Representing 3D rotations

      #include <gandalf/vision/rotate3D.h>

Gandalf has an extensive set of routines for handling 3D rotations. Four different representations are available, defined by the following enumerated type:

      /* types of rotation handled by Gandalf */
      typedef enum { GAN_ROT3D_QUATERNION, GAN_ROT3D_EXPONENTIAL,
                     GAN_ROT3D_ANGLE_AXIS, GAN_ROT3D_MATRIX }
         Gan_Rot3D_Type;

These representations are now described in turn.

The quaternion representation uses the following structure:

      /* quaternion structure */
      typedef struct Gan_Quaternion
      {
         double q0, q1, q2, q3;
      } Gan_Quaternion;

The relationship between a quaternion ${\bf q}=(q_0\;q_1\;q_2\;q_3)^{\top}$ and the equivalent rotation matrix $R$ is

$$R = \left(\!\!\begin{array}{ccc} q_0 q_0 + q_1 q_1-q_2 q_2 ... ..._0 q_0 - q_1 q_1 - q_2 q_2 + q_3 q_3 \end{array}\!\!\right).$$

Here the quaternion is assumed to have been scaled to unit length, i.e. $\vert{\bf q}\vert^2=1$.

The exponential representation uses a 3-vector ${\bf r}$ related to the equivalent rotation matrix $R$ according to

$$R = e^{[{\bf r}]_{\times}}$$

$$= I + \frac{\sin \theta}{\theta} [{\bf r}]_{\times} + \frac{(1-\cos\theta)}{\theta^2} ({\bf r}{\bf r}^{\top}- \Vert{\bf r}\Vert^2 I)$$

where $\theta = \Vert{\bf r}\Vert$ is the rotation angle, and the cross-product matrix $[{\bf r}]_{\times}$ is explained in Section 5.2.

The angle/axis representation $a/{\bf a}$ is strongly related to a quaternion, according to the formula

$${\bf q}= \left(\!\!\begin{array}{c} \cos(a/2) \ a_x\sin(a/2) \ a_y\sin(a/2) \ a_z\sin(a/2) \end{array}\!\!\right)$$

where the rotation axis ${\bf a}=(a_x\;a_y\;a_z)^{\top}$ is assumed to be scaled to $\vert{\bf a}\vert^2=1$. The rotation angle $a$ is measured in radians.

The matrix representation uses a 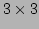$3\times 3$ matrix $R$ as above to represent a rotation

This variety of representations is necessary because of the corresponding variety of operations that can be applied. For instance, quaternions are perhaps the most natural representation, and are a good representation when combining rotations, because quaternion product has a simply linear formula. Given two quaternions ${\bf q}_1=(q_{10}\;q_{11}\;q_{12}\;q_{13})$ and ${\bf q}_2=(q_{20}\;q_{21}\;q_{22}\;q_{23})$, with corresponding rotation matrices $R_1$, $R_2$, the product

$${\bf q}_3 = \left(\!\!\begin{array}{c} q_{10} q_{20} - q_{11... ...q_{20} + q_{11} q_{22} - q_{12} q_{21} \end{array}\!\!\right)$$

is equivalent to the rotation matrix product

$$R_3 = R_1 R_2$$

You should always use quaternions for combining rotations in this way, because if you use matrices the rounding error will accumulate over repeated matrix multiplications, and cause the matrix to become non-orthogonal. With quaternions the scale will drift slightly, but it is much easier to fix the scale of a quaternion than to correct the matrix representation. The angle/axis form is mainly useful as an intuitive way of defining rotations. It has the problem of having no unique representation of zero rotations, since in this case the axis is arbitrary. The exponential representation is unique in being a minimal representation with its three parameters. It is mainly useful however only for small rotations, since it has severe singularity problems for large rotations. For optimisation purposes, you can use the exponential form of rotation to represent a small change in the estimated rotation, with a quaternion used to represent the latest rotation estimate. Similar local coordinate forms of optimisation have been employed in 3D reconstruction by Taylor & Kriegman [#!Taylor:Kriegman:PAMI95!#]. A local rotation representation has also been developed independently by Pennec & Thirion [#!Pennec:Thirion:IJCV97!#]

First we describe some routines specific to the quaternion representation. Then we provide details of how the Gandalf structure Gan_Rot3D is used to create and manipulate rotations of any of the currently supported representations.