Formal Statement of the FHT Plane Fitting Algorithm

We have:

1. A set of disparity points $(x_j , y_j , d_j )$, $j=1 \ldots n$.

2. An array of weights $W_j$, $j=1 \ldots n$, one for each disparity point $(x_j , y_j , d_j )$.

3. Parameter space $(a,b,c)$, restricted to the box with centre $(0,0,d_{\rm centre})$ and side lengths $L_a$, $L_b$ and $L_c$. $d_{\rm centre}$ is the centre of the disparity search range.

4. A vote threshold $T= \theta W$, $W$ being the total weight of the edges in the square patch.

5. A minimum level of subdivision $l_{\min}$ (e.g. 3), and a maximum level $l_{\max}$ (e.g. 10).

The algorithm is as follows:

begin

Declare new variables:

An array ${\bf R}$ of distances $R_j$, $j=1 \ldots n$.

An array ${\bf P}$ of boolean flags $P_1, P_2,\ldots,P_n$ where each $P_j$ either takes the value $true$ or $false$.

Integer variables $max\_level$ and $max\_value$, initialised to zero.

Variables $a_{\rm best}$, $b_{\rm best}$ and $c_{\rm best}$ making up a point in $(a,b,c)$ space.

Another array of boolean flags ${\bf P}_{\rm best}$.

The variables $max\_level$, $max\_value$, $a_{\rm best}$, $b_{\rm best}$, $c_{\rm best}$ and array ${\bf P}_{\rm best}$ are used to keep track of the best fit as the algorithm proceeds.

Set all the $P_j$ to $false$.

For each disparity point $(x_j , y_j , d_j )$:

begin

Calculate the plane parameters for $(X_1 , X_2 , X_3 )$ space:

$$a_{0j} = \frac{-d_j}{Q} ,\; a_{1j} = \frac{L_a x_j}{Q} ,\; a_{2j} = \frac{L_b y_j}{Q} ,\; a_{3j} = \frac{L_c}{Q}$$

where $Q = \sqrt{L_a^2 x_j^2 + L_b^2 y_j^2 + L_c^2}$.

Calculate the normalised perpendicular distance $R_j$ from the plane to the centre of the root cube:

$$R_j = a_{0j} + \sum_{i=1}^3 a_{ij} C_i = a_{0j} + \frac{a_{3j} d_{\rm centre}}{Q L_c}.$$

If $R_j < \frac{\sqrt{3}}{2}$ the plane passes through the root cube's circumscribing sphere: set $P_j$ to $true$.

end

Call the procedure $divide\_cube$ with arguments as follows:

1. Array of boolean flags ${\bf P}$.

2. Array ${\bf R}$ of normalised distances.

3. Initial level of subdivision 0.

4. Initial accumulator value 0.

5. Empty line of descent list.

end

Procedure $divide\_cube$ ( array of flags ${\bf P}$, array of normalised distances ${\bf R}$, subdivision level $l$, accumulator value $v$, line of descent list ):

begin

Declare new variables:

Eight boolean flags arrays ${\bf P}_{\bf b}$, one for each ${\bf b}$, where ${\bf b}$ is a child cube index triplet $(b_1 , b_2 , b_3 )$ and each $b_i$ is either -1 or 1. All the elements of the flag arrays are initialised to $false$.

Eight arrays ${\bf R}_{\bf b}$ of normalised distances.

Accumulators $A_{\bf b}$ for each ${\bf b}$, initialised to zero.

Boolean flag $s$, initialised to $false$.

Sum the votes for the child cubes: for each $j$ such that $P_j = true$:

begin

For each child cube with index b:

begin

Calculate the normalised distance $R_{j {\bf b}}$ from plane $j$ to the centre of the child cube:

$$R_{j {\bf b}} = 2R_j + \frac{1}{2} (a_{1j} b_1 + a_{2j} b_2 + a_{3j} b_3).$$

(The $a_{1j} b_1 + a_{2j} b_2 + a_{3j} b_3$ values can be efficiently calculated by storing them in eight arrays, one for each ${\bf b}$.)

If $R_{j {\bf b}} < \frac{\sqrt{3}}{2}$ then

begin

Add weight $W_j$ to $A_{\bf b}$

Set flag $P_{j {\bf b}}$ to $true$.

end

end

end

Subdivide child cubes receiving greater than or equal to $T$ votes: If $l < l_{\rm max}$:

begin

For each child cube with index b:

begin

If $A_{\bf b} \geq T$ recursively subdivide child cube:

begin

Add ${\bf b}$ to original line of descent.

Call $divide\_cube$ with arguments ${\bf P}_{\bf b}$, ${\bf R}_{\bf b}$, $l+1$, $A_{\bf b}$ and extended line of descent.

Set flag $s$ to $true$.

end

end

end

If $s$ is still $false$ (i.e. no further subdivision of this cube), test for best fit so far:

If $l > max\_level$ or if $l = max\_level$ and $v > max\_value$:

begin

Set $max\_level$ to $l$.

Set $max\_value$ to $v$.

Calculate centre of cube in $(a,b,c)$ space by calling procedure $cube\_centre$ with the line of descent as argument. The results are copied into $a_{\rm best}$, $b_{\rm best}$ and $c_{\rm best}$.

Copy array of flags ${\bf P}$ into array ${\bf P}_{\rm best}$.

end

end (procedure $divide\_cube$)

Procedure $cube\_centre$ ( line of descent list ): begin

Declare new variables:

Three arrays ${\bf r}_a$, ${\bf r}_b$ and ${\bf r}_c$, each of three elements with indices -1, 0 and 1, so that ${\bf r}_a = [r_a(-1),r_a(0),r_a(1)]$ and similarly for ${\bf r}_b$ and ${\bf r}_c$. The zero (middle) elements of each array are not used.

Set arrays ${\bf r}_a$, ${\bf r}_b$ and ${\bf r}_c$ as follows:

$$\begin{array}{ccc} r_a(-1) = \frac{-L_a}{4}, & r_b(-1) = \... ...) = \frac{L_b}{4}, & r_c(1) = \frac{L_c}{4}. \\ \end{array}$$

Set $a_{\rm best}$, $b_{\rm best}$ and $c_{\rm best}$ to zero.

While line of descent not traversed (i.e. root cube not yet reached):

begin

Take next triplet of indices ${\bf b}$ on line of descent.

Replace old values of $a_{\rm best}$, $b_{\rm best}$ and $c_{\rm best}$:

$$\begin{array}{c} a_{\rm best} \leftarrow \frac{a_{\rm best... ... \leftarrow \frac{c_{\rm best}}{2} + r_c(b_3) \\ \end{array}$$

end

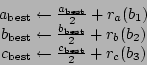
Add centre $c$-coordinate of root cube to $c_{\rm best}$ ($a$ and $b$ coordinates of root are zero):

$$c_{\rm best} \leftarrow c_{\rm best} + d_{\rm centre}$$

end (procedure $cube\_centre$)

At the end of the algorithm $max\_level$ is the highest level of subdivision reached. This must be greater than or equal to $l_{\min}$ for the fit to be used. $max\_value$ is the highest accumulator value of a cube at subdivision level $max\_level$, the cube has centre $(a_{\rm best} , b_{\rm best} , c_{\rm best} )$ and these are the best fit plane parameters. The flags ${\bf P}_{j \rm best}$ are $true$ if the $j$'th disparity point voted for the winning cube, and those disparity points constitute the subset of all the points which best fit a plane, given that the total weight of the points must exceed $T$. They and the values of $max\_level$ and $max\_value$ can stored for use. More precise estimates of the plane parameters can be calculated using orthogonal regression.