



Next: Robust observations
Up: The Vision Package
Previous: Representing 3D Euclidean transformations
Contents
#include <gandalf/vision/lev_marq.h>
The Levenberg-Marquardt
algorithm [#!Marquardt:JSIAM63!#,#!Bjorck:96!#]
is a general non-linear downhill minimisation algorithm
for the case when derivatives of the objective function are known.
It dynamically mixes Gauss-Newton and gradient-descent iterations.
We shall develop the L-M algorithm for a simple
case in our notation, which is derived from Kalman filtering
theory [#!BarShalom:Fortmann:88!#]. The Gandalf implementation of
Levenberg-Marquardt will then be presented. Let the unknown parameters be
represented by the vector 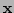 , and let noisy measurements of
, and let noisy measurements of
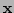 be made:
be made:
 |
(5.7) |
where
 is a measurement function and
is a measurement function and
 is zero-mean
noise with covariance
is zero-mean
noise with covariance
 . Since we are describing an iterative
minimization algorithm, we shall assume that we have already obtained
an estimate
. Since we are describing an iterative
minimization algorithm, we shall assume that we have already obtained
an estimate  of
of 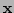 .
Then the maximum likelihood solution for a new estimate
.
Then the maximum likelihood solution for a new estimate 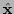 minimizes
minimizes
 |
(5.8) |
We form a quadratic approximation to  around
around  , and minimize
this approximation to
, and minimize
this approximation to  to obtain a new estimate
to obtain a new estimate  .
In general we can write such a quadratic approximation as
.
In general we can write such a quadratic approximation as
for scalar  , vectors
, vectors  ,
, 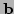 and matrices
and matrices  ,
, 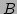 .
Note that here and in equation (5.8) the signs and factors of two
are chosen WLOG to simplify the resulting expressions for the solution.
Differentiating, we obtain
.
Note that here and in equation (5.8) the signs and factors of two
are chosen WLOG to simplify the resulting expressions for the solution.
Differentiating, we obtain
At the minimum point 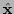 we have
we have
 which means that
which means that
 |
(5.9) |
Thus we need to obtain  and
and  to compute the update.
We now consider the form of
to compute the update.
We now consider the form of  in (5.8).
Writing the Jacobian of
in (5.8).
Writing the Jacobian of
 as
as
we have
In the last formula for
 , the terms
involving the second derivatives of
, the terms
involving the second derivatives of
 have been omitted. This is done because these terms are
generally much smaller and can in practice be omitted, as well as because
the second derivatives are more difficult and complex to compute than the
first derivatives.
have been omitted. This is done because these terms are
generally much smaller and can in practice be omitted, as well as because
the second derivatives are more difficult and complex to compute than the
first derivatives.
Now we solve the above equations for  and
and  given
the values of function
given
the values of function
 and the Jacobian
and the Jacobian
 evaluated at the previous estimate
evaluated at the previous estimate  .
We have immediately
.
We have immediately
We now write the innovation vectors
 as
as
Then we have
 |
(5.12) |
Combining equations (5.9) and (5.12) we
obtain the linear system
 |
(5.13) |
to be solved for the adjustment
 .
The covariance of the state is
.
The covariance of the state is
The update (5.13) may be repeated,
substituting the new  as
as  , and
improving the estimate until convergence is achieved according to some
criterion. Levenberg-Marquardt modifies this updating procedure by
adding a value
, and
improving the estimate until convergence is achieved according to some
criterion. Levenberg-Marquardt modifies this updating procedure by
adding a value  to the diagonal elements of the linear system matrix
before inverting it to obtain the update.
to the diagonal elements of the linear system matrix
before inverting it to obtain the update.
 is reduced if the last iteration gave
an improved estimate, i.e. if
is reduced if the last iteration gave
an improved estimate, i.e. if  was reduced, and increased if
was reduced, and increased if  increased, in which case the estimate of
increased, in which case the estimate of 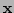 is reset to the
estimate before the last iteration. It is this that allows the algorithm
to smoothly switch between Gauss-Newton (small
is reset to the
estimate before the last iteration. It is this that allows the algorithm
to smoothly switch between Gauss-Newton (small  ) and gradient
descent (large
) and gradient
descent (large  ).
).
This version is a generalization
of Levenberg-Marquardt as it is normally presented
(e.g. [#!Press:etal:88!#]) in that we incorporate vector measurements
 with covariances
with covariances
 , rather than scalar measurements
with variances. The full algorithm is as follows:
, rather than scalar measurements
with variances. The full algorithm is as follows:
- Start with a prior estimate
 of
of 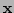 . Initialize
. Initialize  to some starting value, e.g. 0.001.
to some starting value, e.g. 0.001.
- Compute the updated estimate
 by solving the linear
system (5.13) for the adjustment, having first added
by solving the linear
system (5.13) for the adjustment, having first added
 to each diagonal element of
to each diagonal element of  . Note that the Lagrange
multiplier diagonal block should remain at zero.
. Note that the Lagrange
multiplier diagonal block should remain at zero.
- Compute the least-squares residuals
 and
and
 from (5.8).
from (5.8).
- If
 , reduce
, reduce  by a specified factor
(say 10), set
by a specified factor
(say 10), set  to
to  , and return to step 2.
, and return to step 2.
- Otherwise, the update failed to reduce the residual, so increase
 by a factor (say 10), forget the updated
by a factor (say 10), forget the updated  and
return to step 2.
and
return to step 2.
The algorithm continues until some pre-specified termination criterion
has been met, such as a small change to the state vector, or a limit on
the number of iterations.
If the measurements
 are unbiased and normally distributed,
the residual
are unbiased and normally distributed,
the residual
 is a
is a 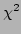 random variable, and testing
the value of
random variable, and testing
the value of  against a
against a 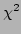 distribution is a good way
of checking that the measurement noise model is reasonable.
The number of degrees of freedom (DOF) of the
distribution is a good way
of checking that the measurement noise model is reasonable.
The number of degrees of freedom (DOF) of the 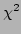 distribution
can be determined as the total size of the measurement vectors,
minus the size of the state.
If the
distribution
can be determined as the total size of the measurement vectors,
minus the size of the state.
If the  function returns the dimension of its vector
argument, then the degrees of freedom may be computed as
function returns the dimension of its vector
argument, then the degrees of freedom may be computed as
 |
(5.14) |
Subsections




Next: Robust observations
Up: The Vision Package
Previous: Representing 3D Euclidean transformations
Contents
2006-03-17
![]() and
and ![]() given
the values of function
given
the values of function
![]() and the Jacobian
and the Jacobian
![]() evaluated at the previous estimate
evaluated at the previous estimate ![]() .
We have immediately
.
We have immediately

![]() as
as ![]() , and
improving the estimate until convergence is achieved according to some
criterion. Levenberg-Marquardt modifies this updating procedure by
adding a value
, and
improving the estimate until convergence is achieved according to some
criterion. Levenberg-Marquardt modifies this updating procedure by
adding a value ![]() to the diagonal elements of the linear system matrix
before inverting it to obtain the update.
to the diagonal elements of the linear system matrix
before inverting it to obtain the update.
![]() is reduced if the last iteration gave
an improved estimate, i.e. if
is reduced if the last iteration gave
an improved estimate, i.e. if ![]() was reduced, and increased if
was reduced, and increased if ![]() increased, in which case the estimate of
increased, in which case the estimate of ![]() is reset to the
estimate before the last iteration. It is this that allows the algorithm
to smoothly switch between Gauss-Newton (small
is reset to the
estimate before the last iteration. It is this that allows the algorithm
to smoothly switch between Gauss-Newton (small ![]() ) and gradient
descent (large
) and gradient
descent (large ![]() ).
).
![]() with covariances
with covariances
![]() , rather than scalar measurements
with variances. The full algorithm is as follows:
, rather than scalar measurements
with variances. The full algorithm is as follows:
![]() are unbiased and normally distributed,
the residual
are unbiased and normally distributed,
the residual
![]() is a
is a ![]() random variable, and testing
the value of
random variable, and testing
the value of ![]() against a
against a ![]() distribution is a good way
of checking that the measurement noise model is reasonable.
The number of degrees of freedom (DOF) of the
distribution is a good way
of checking that the measurement noise model is reasonable.
The number of degrees of freedom (DOF) of the ![]() distribution
can be determined as the total size of the measurement vectors,
minus the size of the state.
If the
distribution
can be determined as the total size of the measurement vectors,
minus the size of the state.
If the ![]() function returns the dimension of its vector
argument, then the degrees of freedom may be computed as
function returns the dimension of its vector
argument, then the degrees of freedom may be computed as