Levenberg-Marquardt software

The following code extracts are taken from the vision/vision_test.c test program. The example application is fitting a quadratic function through points $x,y$ on a plane. The function to be fitted is

$$y = ax^2 + bx + c$$

The state vector of unknown parameters to be estimated is thus

$${\bf x}= \left(\!\!\begin{array}{c} a \ b \ c \end{array}\!\!\right)$$

and we wish to compute the least-squares solution that minimises

$$J({\bf x}) = \sum_{j=1}^k(y_j - ax_j^2 - bx_j - c)^2 \sigma_j^{-2}$$

given $k$ points $x_j,y_j$ for $j=1,\ldots,k$ and independent noise levels $\sigma_j$ for each point $j$. This can be solved directly by linear methods, and this feature makes it useful as a test algorithm because test program can compare the results with the Levenberg-Marquardt solution. The problem can be put into the form of the Levenberg-Marquardt algorithm described above by identifying

$${\bf z}{\scriptstyle (j)}= (y_j),\;\;\;N^{-1}{\scriptstyle (j)}= (\sigma^{-2}),\;\;\; {\bf h}({\bf x}) = ax_j^2 + bx_j + c$$

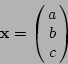
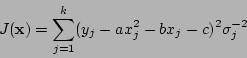
To initialise a Levenberg-Marquardt algorithm instance use the call

      Gan_LevMarqStruct *lm;

      /* initialise Levenberg-Marquardt algorithm */
      lm = gan_lev_marq_alloc();

We build the points from ground-truth values for the quadratic coefficients $a,b,c$, and add random Gaussian noise:

      /* number of points */
      #define NPOINTS 100

      /* ground-truth quadratic coefficients a,b,c */
      #define A_TRUE 2.0
      #define B_TRUE 3.0
      #define C_TRUE 4.0

      /* noise standard deviation */
      #define SIGMA 1.0

      /* arrays of x & y coordinates */
      double xcoord[NPOINTS], ycoord[NPOINTS];

      /* build arrays of x & y coordinates */
      for ( i = NPOINTS-1; i >= 0; i-- )
      {
         /* x-coordinates evenly spaced */
         xcoord[i] = (double) i;

         /* construct y = a*x^2 + b*y + c + w with added Gaussian noise w */
         ycoord[i] = A_TRUE*xcoord[i]*xcoord[i] + B_TRUE*xcoord[i]
                     + C_TRUE + gan_normal_sample(0.0, SIGMA);
      }

Here we defined a noise level SIGMA as the estimated standard deviation of the random observation errors, the same for each point. Now that we have constructed the input data, the next thing is to create observations for each point. Gandalf's version of Levenberg-Marquardt uses callback functions to evaluate observation ${\bf h}(.)$ and observation Jacobians $H$. A non-robust h-type observation is then defined by:

• The observation vector ${\bf z}$;
• The observation inverse covariance $N^{-1}$, and;
• The observation callback function ${\bf h}(.)$.

We construct the observations for the quadratic fitting problem using the following code:

      Gan_Vector *z; /* define observation vector */
      Gan_SquMatrix *Ni; /* define observation inverse covariance */

      /* allocate observation vector z and inverse covariance Ni */
      z = gan_vec_alloc(1);
      Ni = gan_symmat_fill_va ( NULL, 1, 1.0/(SIGMA*SIGMA) );

      for ( i = NPOINTS-1; i >= 0; i-- )
      {
         /* construct point observation */
         z = gan_vec_fill_va ( z, 1, ycoord[i] );
         cu_assert ( z != NULL );
         cu_assert ( gan_lev_marq_obs_h ( lm, z, &xcoord[i], Ni, quadratic_h )
                     != NULL );
      }

We create the observation vector with size one; this can be adjusted dynamically if necessary; see Section 3.2.1.2.

The observation callback function quadratic_h() is defined as follows:

      /* observation callback function for single point */
      static Gan_Bool
       quadratic_h ( Gan_Vector *x,  /* state vector */
                     Gan_Vector *z,  /* observation vector */
                     void *zdata,    /* user pointer attached to z */
                     Gan_Vector *h,  /* vector h(x) to be evaluated */
                     Gan_Matrix *H ) /* matrix dh/dx to be evaulated or NULL */
      {
         double a, b, c;

         /* read x-coordinate from user-defined data pointer */
         double xj = *((double *) zdata);

         /* read quadratic parameters from state vector x=(a b c)^T*/
         if ( !gan_vec_read_va ( x, 3, &a, &b, &c ) )
         {
            gan_err_register ( "quadratic_h", GAN_ERROR_FAILURE, NULL );
            return GAN_FALSE;
         }

         /* evaluate h(x) = h(a,b,c) = y = a*x*x + b*x + c */
         if ( gan_vec_fill_va ( h, 1, a*xj*xj + b*xj + c ) == NULL )
         {
            gan_err_register ( "quadratic_h", GAN_ERROR_FAILURE, NULL );
            return GAN_FALSE;
         }

         /* if Jacobian matrix is passed as non-NULL, fill it with the Jacobian
            matrix (dh/da dh/db dh/dc) = (x*x x 1) */
         if ( H != NULL &&
              gan_mat_fill_va ( H, 1, 3, xj*xj, xj, 1.0 ) == NULL )
         {
            gan_err_register ( "quadratic_h", GAN_ERROR_FAILURE, NULL );
            return GAN_FALSE;
         }

         /* success */
         return GAN_TRUE;
      }

Note the the $x$-coordinate passed in as the third ``user pointer'' argument to gan_lev_marq_obs_h() is read into the variable xj in quadratic_h(). Using pointers in this way is the standard method to pass extra information into the callback routines.

So far we have merely registered the observations and their callback routines. No processing has started. To get started with some actual optimisation we need to initialise the state vector with some values for $a$, $b$ and $c$. This involves invoking the routine

      double residual;

      /* initialise Levenberg-Marquardt algorithm */
      gan_lev_marq_init ( lm, quadratic_init, NULL, &residual );

quadratic_init() is another callback routine that computes values for the state vector ${\bf x}$ given the observations ${\bf z}{\scriptstyle (j)}$. The observations are presented to quadratic_init() in a linked list. The third argument to gan_lev_marq_init() is another user pointer, not used in this example. The last residual argument is returned as the initial value of the least-squares residual $J({\bf x})$. This is the full code for the quadratic_init() function, whose operation is self-explanatory:

      /* initialisation function for state vector */
      static Gan_Bool
       quadratic_init ( Gan_Vector *x0,     /* state vector to be initialised */
                        Gan_List *obs_list, /* list of observations */
                        void *data )        /* user data pointer */
      {
         int list_size = gan_list_get_size(obs_list);
         Gan_LevMarqObs *obs;
         Gan_Matrix33 A;
         Gan_Vector3 b;
         double xj, y;

         /* we need at least three points to fit a quadratic */
         if ( list_size < 3 ) return GAN_FALSE;

         /* initialise quadratic by interpolating three points: the first, middle and
            last point in the list of point observations. We construct equations
      
               (y1)   (x1*x1 x1 1) (a)
               (y2) = (x2*x2 x2 1) (b) = A * b for 3x3 matrix A and 3-vector b
               (y3)   (x3*x3 x3 1) (c)

            and solve the equations by direct matrix inversion (not pretty...) to
            obtain our first estimate of a, b, c given points (x1,y1), (x2,y2) and
            (x3,y3).
         */

         /* first point */
         gan_list_goto_pos ( obs_list, 0 );
         obs = gan_list_get_current ( obs_list, Gan_LevMarqObs );
         xj = *((double *) obs->details.h.zdata); /* read x-coordinate */
         A.xx = xj*xj; A.xy = xj; A.xz = 1.0; /* fill first row of equations in A */
         gan_vec_read_va ( &obs->details.h.z, 1, &y );
         b.x = y; /* fill first entry in b vector */
    
         /* middle point */
         gan_list_goto_pos ( obs_list, list_size/2 );
         obs = gan_list_get_current ( obs_list, Gan_LevMarqObs );
         xj = *((double *) obs->details.h.zdata); /* read x-coordinate */
         A.yx = xj*xj; A.yy = xj; A.yz = 1.0; /* fill first row of equations in A */
         gan_vec_read_va ( &obs->details.h.z, 1, &y );
         b.y = y; /* fill second entry in b vector */
    
         /* last point */
         gan_list_goto_pos ( obs_list, list_size-1 );
         obs = gan_list_get_current ( obs_list, Gan_LevMarqObs );
         xj = *((double *) obs->details.h.zdata); /* read x-coordinate */
         A.zx = xj*xj; A.zy = xj; A.zz = 1.0; /* fill first row of equations in A */
         gan_vec_read_va ( &obs->details.h.z, 1, &y );
         b.z = y; /* fill second entry in b vector */

         /* invert matrix and solve (don't do this at home) */
         A = gan_mat33_invert_s(&A);
         b = gan_mat33_multv3_s ( &A, &b );

         /* fill state vector x0 with our initial values for a,b,c */
         gan_vec_fill_va ( x0, 3, b.x, b.y, b.z );
         return GAN_TRUE;
      }

We are now ready to apply optimisation iterations using the routine gan_lev_marq_iteration(). The following code applies ten iterations, adjusting the damping factor in the way suggested in [#!Press:etal:88!#]. This simple scheme decreases the damping when the residual decreases, and vice versa.

      double lambda = 0.1; /* damping factor */
      double new_residual;

      /* apply iterations */
      for ( i = 0; i < 10; i++ )
      {
         gan_lev_marq_iteration ( lm, lambda, &new_residual );
         if ( new_residual < residual )
         {
            /* iteration succeeded in reducing the residual */
            lambda /= 10.0;
            residual = new_residual;
         }
         else
            /* iteration failed to reduce the residual */
            lambda *= 10.0;
      }

To extract the optimised solution, use the code

   Gan_Vector *x;

   /* get optimised solution */
   x = gan_lev_marq_get_x ( lm );

Note that the x pointer passed back here points to a vector internal to the Levenberg-Marquardt software, and should not be freed. To free the Levenberg-Marquardt structure and the matrices & vectors created above, use the code

   gan_squmat_free ( Ni );
   gan_vec_free ( z );
   gan_lev_marq_free ( lm );