Notation

Next: The FHT Algorithm Up: The Fast Hough Transform Previous: The Fast Hough Transform Contents

Notation

The following notation is taken from [#!Li_etc_86!#]. Hyperplanes are represented by the equations

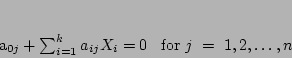$\begin{displaymath} a_{0j} + \sum_{i=1}^k a_{ij} X_i = 0\;\;\;{\rm for} j = 1,2,\ldots,n \end{displaymath}$

(5.15)

where 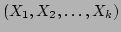$(X_1,X_2,\ldots, X_k)$ is parameter space, rescaled so that the initial ranges of each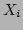

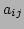are the same and centred around zero. The initial ranges thus form a hypercube (generalisation of a cube) in parameter space. Each $a_{ij}$ is a function of

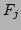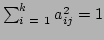normalised such that $\sum_{i = 1}^k a_{ij}^2 = 1$ .

2006-03-17