Filling a general size matrix with values

To fill a matrix with values, create the matrix and then use the routine gan_mat_fill_va(). An example is

      Gan_Matrix mA;

      /* ... create mA using e.g. gan_mat_form() ... */
      gan_mat_fill_va ( &mA, 2, 3, 1.0, 2.0, 3.0,
                                   4.0, 5.0, 6.0 );

which sets matrix mA to have dimensions 2 rows by 3 columns, and sets the value to

$$A = \left(\!\!\begin{array}{ccc} 1 & 2 & 3 \ 4 & 5 & 6 \end{array}\!\!\right)$$

To fill a matrix with a constant value, you can use

      gan_mat_fill_const_q ( &mA, 4, 2, 3.0 );

which sets the dimensions of mA to four rows by two columns, and sets all the elements to three. This gives rise to the matrix

$$A = \left(\!\!\begin{array}{cccc} 3 & 3 & 3 & 3 \ 3 & 3 & 3 & 3 \end{array}\!\!\right)$$

This function is also available in a form which allocates and fills a matrix from scratch:

      Gan_Matrix *pmA;

      pmA = gan_mat_fill_const_s ( 4, 2, 3.0 );

There are special macro routines for setting a matrix to zero:

      gan_mat_fill_zero_q ( &mA, 4, 2 ); /* OR */
      pmA = gan_mat_fill_zero_s ( 4, 2 );

For square matrices there are specific routines for each square matrix type. The order in which the elements are passed in the variable argument list corresponds to the matrix type. For symmetric matrice, only the lower triangle is passed (including the diagonal). So for instance to create a symmetric matrix

$$S = \left(\!\!\begin{array}{ccc} 1 & 2 & 4 \ 2 & 3 & 5 \ 4 & 5 & 6\end{array}\!\!\right)$$

use the code

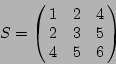
      Gan_SquMatrix smS;

      /* ... create smS using e.g. gan_symmat_form() ... */
      gan_symmat_fill_va ( &smS, 3, 1.0,
                                    2.0, 3.0,
                                    4.0, 5.0, 6.0 );

For lower and upper triangular matrices pass the elements in the relevant order for the corresponding triangle. So for instance

      Gan_SquMatrix smL;

      /* ... create smL using e.g. gan_ltmat_form() ... */
      gan_ltmat_fill_va ( &smL, 3, 1.0,
                                   2.0, 3.0,
                                   4.0, 5.0, 6.0 );

creates the lower triangular matrix

$$L = \left(\!\!\begin{array}{ccc} 1 & 0 & 0 \ 2 & 3 & 0 \ 4 & 5 & 6\end{array}\!\!\right)$$

while

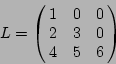
      Gan_SquMatrix smU;

      /* ... create smU using e.g. gan_utmat_form() ... */
      gan_utmat_fill_va ( &smU, 3, 1.0, 2.0, 4.0,
                                        3.0, 5.0,
                                             6.0 );

creates the upper triangular matrix

$$U = \left(\!\!\begin{array}{ccc} 1 & 2 & 4 \ 0 & 3 & 5 \ 0 & 0 & 6 \end{array}\!\!\right)$$

The routines for diagonal and scaled identity matrices follow a similar pattern, so you can use

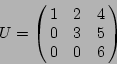
      Gan_SquMatrix smD;

      /* ... create smD using e.g. gan_diagmat_form() ... */
      gan_diagmat_fill_va ( &smD, 4, 1.0, 2.0, 3.0, 4.0 );

to create the diagonal matrix

$$D = \left(\!\!\begin{array}{cccc} 1 & 0 & 0 & 0 \ 0 & 2 & 0 & 0 \ 0 & 0 & 3 & 0 \ 0 & 0 & 0 & 4 \end{array}\!\!\right)$$

or

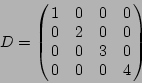
      Gan_SquMatrix smsI;

      /* ... create smsI using e.g. gan_scalImat_form() ... */
      gan_scalImat_fill_va ( &msI, 4, 2.0 );

to create the scaled identity matrix

$$D = \left(\!\!\begin{array}{cccc} 2 & 0 & 0 & 0 \ 0 & 2 & 0 & 0 \ 0 & 0 & 2 & 0 \ 0 & 0 & 0 & 2 \end{array}\!\!\right)$$

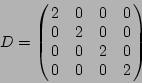
There are also routines to fill square matrices with a constant value, with a special routine for filling with zero:

      Gan_SquMatrix smA;

      /* ... create smA using e.g. gan_squmat_form() ... */
      gan_symmat_fill_const_q ( &smA, 4, 3.0 ); /* set A as symmetric(4x4), each element 3 */
      gan_ltmat_fill_const_q ( &smA, 4, 3.0 ); /* set A as l. triang.(4x4), each element 3 */
      gan_utmat_fill_const_q ( &smA, 4, 3.0 ); /* set A as u. triang.(4x4), each element 3 */
      gan_diagmat_fill_const_q ( &smA, 4, 3.0 ); /* set A as diagonal(4x4), each element 3 */
      gan_scalImat_fill_const_q ( &smA, 4, 3.0 ); /* set A as scaled I(4x4), each element 3 */
      gan_symmat_fill_zero_q ( &smA, 4 ); /* set A as symmetric(4x4), each element zero */
      gan_ltmat_fill_zero_q ( &smA, 4 ); /* set A as l. triang.(4x4), each element zero */
      gan_utmat_fill_zero_q ( &smA, 4 ); /* set A as u. triang.(4x4), each element zero */
      gan_diagmat_fill_zero_q ( &smA, 4 ); /* set A as diagonal(4x4), each element zero */
      gan_scalImat_fill_zero_q ( &smA, 4 ); /* set A as scaled I(4x4), each element zero */

set the type and size of an existing square matrix, and sets all its elements to the same value,

      Gan_SquMatrix *psmS, *psmL, *psmU, *psmD, *psmsI;

      psmS = gan_symmat_fill_const_s ( 4, 3.0 ); /* create 4x4 symmetric mat., each el. 3 */
      psmL = gan_ltmat_fill_const_s ( 4, 3.0 ); /* create 4x4 u. tri. mat., each el. 3 */
      psmU = gan_utmat_fill_const_s ( 4, 3.0 ); /* create 4x4 l. tri. mat., each el. 3 */
      psmD = gan_diagmat_fill_const_s ( 4, 3.0 ); /* create 4x4 diagonal mat., each el. 3 */
      psmsI = gan_scalImat_fill_const_s ( 4, 3.0 ); /* create 4x4 scaled I mat., each el. 3 */
      psmS = gan_symmat_fill_zero_s ( 4 ); /* create 4x4 symmetric mat., each el. zero */
      psmL = gan_ltmat_fill_zero_s ( 4 ); /* create 4x4 u. tri. mat., each el. zero */
      psmU = gan_utmat_fill_zero_s ( 4 ); /* create 4x4 l. tri. mat., each el. zero */
      psmD = gan_diagmat_fill_zero_s ( 4 ); /* create 4x4 diagonal mat., each el. zero */
      psmsI = gan_scalImat_fill_zero_s ( 4 ); /* create 4x4 scaled I mat., each el. zero */

create new matrices with the given type and size, and set all the elements to the same value,

There are also equivalent routines that work with a variable square matrix type:

      Gan_SquMatrix smA, *psmA;
      Gan_SquMatrixType type;

      /* ... create smA using e.g. gan_squmat_form() and set type to
             desired square matrix type, e.g. GAN_SYMMETRIC_MATRIX ...*/

      /* set up an existing matrix, fill it with a constant value */
      gan_squmat_fill_const_q ( &smA, type, 4, 3.0 ); /* constant element value 3 */
      gan_squmat_fill_zero_q ( &smA, type, 4 ); /* fill with zero */

      /* create a matrix from scratch */
      psmA = gan_squmat_fill_const_s ( type, 4, 3.0 ); /* constant element value 3 */
      psmA = gan_squmat_fill_const_s ( type, 4, 3.0 ); /* fill with zero */

Note that the dynamic reconfiguration feature of square matrices means again that the ..._fill_va(),
.._fill_const_q() and ..._fill_zero_q() square matrix routines do not require the matrix to be set up initially with either the same type or size.

Error detection: NULL is returned and the error handler is invoked on failure. The most likely failure mode is failing to reallocate the matrix data when the size of the matrix is changed, i.e. failure of a call to realloc().