



Next: Levenberg-Marquardt software
Up: Levenberg-Marquardt minimisation
Previous: Robust observations
Contents
The observation function 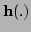 in Equation 5.7
does not encapsulate the most general
form of observation, since it assumes that the observation vector
in Equation 5.7
does not encapsulate the most general
form of observation, since it assumes that the observation vector 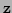 can be separated as a function of the state
can be separated as a function of the state 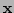 . It is sometimes therefore
necessary to introduce a generalised observation of the form
. It is sometimes therefore
necessary to introduce a generalised observation of the form
where 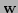 again represents a random noise vector having covariance
again represents a random noise vector having covariance 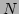 .
However with some manipulation and extra computation we can effectively
convert the linearised version of the
.
However with some manipulation and extra computation we can effectively
convert the linearised version of the 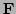 -type function into an
-type function into an
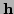 -type function, allowing it to be incorporated in the same way.
We linearise
-type function, allowing it to be incorporated in the same way.
We linearise 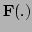 with respect to
with respect to 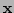 and
and 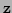 around the
estimated state
around the
estimated state 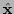 and observation
and observation 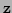 , assuming
that the noise
, assuming
that the noise 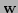 is small:
is small:
where 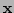 here represents the true value of the state vector, and
here represents the true value of the state vector, and 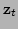 is the true observation vector (as opposed to the actually measured vector
is the true observation vector (as opposed to the actually measured vector
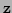 ), so that
), so that
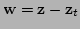 .
We identify the following quantities with their equivalents for an
.
We identify the following quantities with their equivalents for an 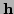 -type
observation:
-type
observation:
- The innovation vector is
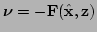 .
.
- The Jacobian matrix is
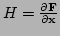 .
.
- The noise vector is
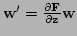 .
.
- The noise covariance matrix is
 .
.
Extra computation is therefore needed to convert the observation covariance
from 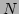 to
to 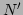 . The innovation vector
. The innovation vector
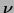 , Jacobian matrix
, Jacobian matrix 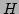 and
observation covariance
and
observation covariance 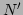 are substituted into the Levenberg-Marquardt
algorithm in place of their equivalents for the
are substituted into the Levenberg-Marquardt
algorithm in place of their equivalents for the 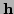 -type observation.
There is no reason why there should not be a robust version of the
-type observation.
There is no reason why there should not be a robust version of the 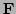 -type
observation, but currently it is not implemented.
-type
observation, but currently it is not implemented.




Next: Levenberg-Marquardt software
Up: Levenberg-Marquardt minimisation
Previous: Robust observations
Contents
2006-03-17