Next: Example: Plane Fitting
Up: The Fast Hough Transform
Previous: The FHT Algorithm
Contents
Example: Line Fitting
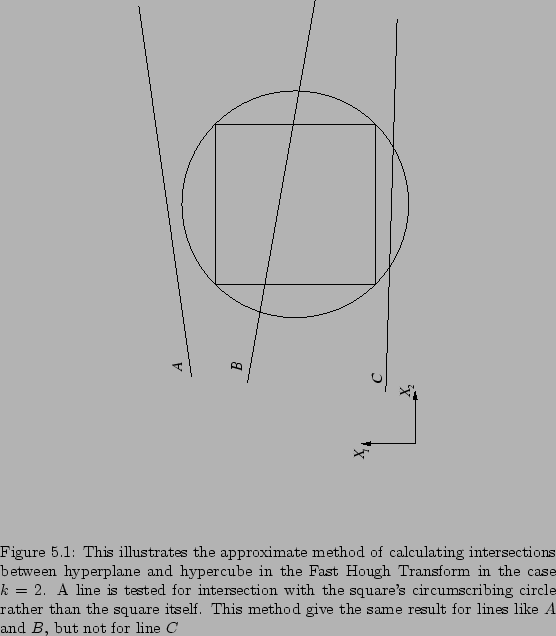
Figure 5.5
shows how the FHT works for 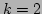 , when parameter space is a plane,
hyperplanes are straight lines and hypercubes are squares whose associated
hyperspheres are circles passing through the vertices of the squares
(figure 5.5).
This is applicable to the
problem of finding a straight line through points on a plane. If the
plane has coordinates
, when parameter space is a plane,
hyperplanes are straight lines and hypercubes are squares whose associated
hyperspheres are circles passing through the vertices of the squares
(figure 5.5).
This is applicable to the
problem of finding a straight line through points on a plane. If the
plane has coordinates 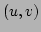 the line can be written
the line can be written
where  and
and  are constant. Each point
are constant. Each point
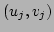 votes for a line in parameter space:
votes for a line in parameter space:
Let the initial ranges of  and
and  , defining the root
hypercube, be
, defining the root
hypercube, be 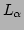 and
and
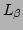 centred around
centred around 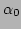 and
and 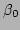 respectively.
Then the above equation can put in the form of
equation 5.15 using the transformation
respectively.
Then the above equation can put in the form of
equation 5.15 using the transformation
where
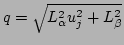 .
.
2006-03-17