Main Page | Modules | Class List | File List | Class Members | File Members

Projective Normalisation of Fixed Size Matrices
[Fixed Size Matrices]


Defines

#define GAN_MAT_NORMALISE   gan_mat22_normalize
#define GAN_MAT_NORM_FNAME   "gan_mat22_normalize"
#define GAN_MATT_NORMALISE   gan_mat22T_normalize
#define GAN_MATT_NORM_FNAME   "gan_mat22T_normalize"
#define GAN_MATTYPE   Gan_Matrix22
#define GAN_SQUMATTYPE   Gan_SquMatrix22
#define GAN_SQUMATTYPEP   Gan_SquMatrix22
#define GAN_MAT_SCALE_S   gan_mat22_scale_s
#define GAN_MAT_DIVIDE_S   gan_mat22_divide_s
#define GAN_MAT_FNORM_S   gan_mat22_Fnorm_s
#define GAN_SYMMAT_IDENT_S   gan_symmat22_ident_s
#define GAN_SYMMAT_INVERT_Q   gan_symmat22_invert_q
#define GAN_SYMMAT_ZERO_Q   gan_symmat22_zero_q
#define GAN_SYMMAT_MULTV_Q   gan_symmat22_multv2_q
#define GAN_SYMMAT_DIVIDE_S   gan_symmat22_divide_s
#define GAN_SYMMAT_DIVIDE_I   gan_symmat22_divide_i
#define GAN_SYMMAT_INCREMENT   gan_symmat22_increment
#define GAN_SYMMAT_TRACE_S   gan_symmat22_trace_s
#define GAN_SYMMAT_SUB_Q   gan_symmat22_sub_q
#define GAN_SYMMAT_SUMSQR_Q   gan_symmat22_sumsqr_q
#define GAN_SYMMAT_CHOLESKY_Q   gan_symmat22_cholesky_q
#define GAN_SYMMAT_LRMULTM_Q   gan_symmat22_lrmultm22_q
#define GAN_SYMMATP_TRACE_S   gan_symmat22_trace_s
#define GAN_LTMATI_MULTV_S   gan_ltmat22I_multv2_s
#define GAN_MAT_RMULTLIT_S   gan_mat22_rmultl22IT_s
#define GAN_MAT_RMULTLIT_S   gan_mat22_rmultl22IT_s
#define GAN_MAT_SLMULTT_Q   gan_mat22_slmultT_q
#define GAN_MAT_TPOSE_I   gan_mat22_tpose_i
#define GAN_MAT_NORMALISE   gan_mat23_normalize
#define GAN_MAT_NORM_FNAME   "gan_mat23_normalize"
#define GAN_MATTYPE   Gan_Matrix23
#define GAN_SQUMATTYPE   Gan_SquMatrix33
#define GAN_SQUMATTYPEP   Gan_SquMatrix22
#define GAN_MAT_SCALE_S   gan_mat23_scale_s
#define GAN_MAT_DIVIDE_S   gan_mat23_divide_s
#define GAN_MAT_FNORM_S   gan_mat23_Fnorm_s
#define GAN_SYMMAT_IDENT_S   gan_symmat33_ident_s
#define GAN_SYMMAT_INVERT_Q   gan_symmat33_invert_q
#define GAN_SYMMAT_ZERO_Q   gan_symmat33_zero_q
#define GAN_SYMMAT_MULTV_Q   gan_symmat33_multv2_q
#define GAN_SYMMAT_DIVIDE_S   gan_symmat33_divide_s
#define GAN_SYMMAT_DIVIDE_I   gan_symmat33_divide_i
#define GAN_SYMMAT_INCREMENT   gan_symmat33_increment
#define GAN_SYMMAT_TRACE_S   gan_symmat33_trace_s
#define GAN_SYMMAT_SUB_Q   gan_symmat33_sub_q
#define GAN_SYMMAT_SUMSQR_Q   gan_symmat33_sumsqr_q
#define GAN_SYMMAT_CHOLESKY_Q   gan_symmat33_cholesky_q
#define GAN_SYMMATP_TRACE_S   gan_symmat22_trace_s
#define GAN_SYMMAT_LRMULTM_Q   gan_symmat33_lrmultm23_q
#define GAN_LTMATI_MULTV_S   gan_ltmat33I_multv2_s
#define GAN_MAT_RMULTLIT_S   gan_mat23_rmultl33IT_s
#define GAN_MAT_RMULTLIT_S   gan_mat23_rmultl33IT_s
#define GAN_MAT_SLMULTT_Q   gan_mat23_slmultT_q
#define GAN_MAT_TPOSE_I   gan_mat23_tpose_i
#define GAN_MAT_NORMALISE   gan_mat24_normalize
#define GAN_MAT_NORM_FNAME   "gan_mat24_normalize"
#define GAN_MATTYPE   Gan_Matrix24
#define GAN_SQUMATTYPE   Gan_SquMatrix44
#define GAN_SQUMATTYPEP   Gan_SquMatrix22
#define GAN_MAT_SCALE_S   gan_mat24_scale_s
#define GAN_MAT_DIVIDE_S   gan_mat24_divide_s
#define GAN_MAT_FNORM_S   gan_mat24_Fnorm_s
#define GAN_SYMMAT_IDENT_S   gan_symmat44_ident_s
#define GAN_SYMMAT_INVERT_Q   gan_symmat44_invert_q
#define GAN_SYMMAT_ZERO_Q   gan_symmat44_zero_q
#define GAN_SYMMAT_MULTV_Q   gan_symmat44_multv2_q
#define GAN_SYMMAT_DIVIDE_S   gan_symmat44_divide_s
#define GAN_SYMMAT_DIVIDE_I   gan_symmat44_divide_i
#define GAN_SYMMAT_INCREMENT   gan_symmat44_increment
#define GAN_SYMMAT_TRACE_S   gan_symmat44_trace_s
#define GAN_SYMMAT_SUB_Q   gan_symmat44_sub_q
#define GAN_SYMMAT_SUMSQR_Q   gan_symmat44_sumsqr_q
#define GAN_SYMMAT_CHOLESKY_Q   gan_symmat44_cholesky_q
#define GAN_SYMMATP_TRACE_S   gan_symmat22_trace_s
#define GAN_SYMMAT_LRMULTM_Q   gan_symmat44_lrmultm24_q
#define GAN_LTMATI_MULTV_S   gan_ltmat44I_multv2_s
#define GAN_MAT_RMULTLIT_S   gan_mat24_rmultl44IT_s
#define GAN_MAT_RMULTLIT_S   gan_mat24_rmultl44IT_s
#define GAN_MAT_SLMULTT_Q   gan_mat24_slmultT_q
#define GAN_MAT_TPOSE_I   gan_mat24_tpose_i
#define GAN_MAT_NORMALISE   gan_mat33_normalize
#define GAN_MAT_NORM_FNAME   "gan_mat33_normalize"
#define GAN_MATT_NORMALISE   gan_mat33T_normalize
#define GAN_MATT_NORM_FNAME   "gan_mat33T_normalize"
#define GAN_MATTYPE   Gan_Matrix33
#define GAN_SQUMATTYPE   Gan_SquMatrix33
#define GAN_SQUMATTYPEP   Gan_SquMatrix33
#define GAN_MAT_SCALE_S   gan_mat33_scale_s
#define GAN_MAT_DIVIDE_S   gan_mat33_divide_s
#define GAN_MAT_FNORM_S   gan_mat33_Fnorm_s
#define GAN_SYMMAT_IDENT_S   gan_symmat33_ident_s
#define GAN_SYMMAT_INVERT_Q   gan_symmat33_invert_q
#define GAN_SYMMAT_ZERO_Q   gan_symmat33_zero_q
#define GAN_SYMMAT_MULTV_Q   gan_symmat33_multv3_q
#define GAN_SYMMAT_DIVIDE_S   gan_symmat33_divide_s
#define GAN_SYMMAT_DIVIDE_I   gan_symmat33_divide_i
#define GAN_SYMMAT_INCREMENT   gan_symmat33_increment
#define GAN_SYMMAT_TRACE_S   gan_symmat33_trace_s
#define GAN_SYMMAT_SUB_Q   gan_symmat33_sub_q
#define GAN_SYMMAT_SUMSQR_Q   gan_symmat33_sumsqr_q
#define GAN_SYMMAT_CHOLESKY_Q   gan_symmat33_cholesky_q
#define GAN_SYMMATP_TRACE_S   gan_symmat33_trace_s
#define GAN_SYMMAT_LRMULTM_Q   gan_symmat33_lrmultm33_q
#define GAN_LTMATI_MULTV_S   gan_ltmat33I_multv3_s
#define GAN_MAT_RMULTLIT_S   gan_mat33_rmultl33IT_s
#define GAN_MAT_RMULTLIT_S   gan_mat33_rmultl33IT_s
#define GAN_MAT_SLMULTT_Q   gan_mat33_slmultT_q
#define GAN_MAT_TPOSE_I   gan_mat33_tpose_i
#define GAN_MAT_NORMALISE   gan_mat34_normalize
#define GAN_MAT_NORM_FNAME   "gan_mat34_normalize"
#define GAN_MATTYPE   Gan_Matrix34
#define GAN_SQUMATTYPE   Gan_SquMatrix44
#define GAN_SQUMATTYPEP   Gan_SquMatrix33
#define GAN_MAT_SCALE_S   gan_mat34_scale_s
#define GAN_MAT_DIVIDE_S   gan_mat34_divide_s
#define GAN_MAT_FNORM_S   gan_mat34_Fnorm_s
#define GAN_SYMMAT_IDENT_S   gan_symmat44_ident_s
#define GAN_SYMMAT_INVERT_Q   gan_symmat44_invert_q
#define GAN_SYMMAT_ZERO_Q   gan_symmat44_zero_q
#define GAN_SYMMAT_MULTV_Q   gan_symmat44_multv3_q
#define GAN_SYMMAT_DIVIDE_S   gan_symmat44_divide_s
#define GAN_SYMMAT_DIVIDE_I   gan_symmat44_divide_i
#define GAN_SYMMAT_INCREMENT   gan_symmat44_increment
#define GAN_SYMMAT_TRACE_S   gan_symmat44_trace_s
#define GAN_SYMMAT_SUB_Q   gan_symmat44_sub_q
#define GAN_SYMMAT_SUMSQR_Q   gan_symmat44_sumsqr_q
#define GAN_SYMMAT_CHOLESKY_Q   gan_symmat44_cholesky_q
#define GAN_SYMMATP_TRACE_S   gan_symmat33_trace_s
#define GAN_SYMMAT_LRMULTM_Q   gan_symmat44_lrmultm34_q
#define GAN_LTMATI_MULTV_S   gan_ltmat44I_multv3_s
#define GAN_MAT_RMULTLIT_S   gan_mat34_rmultl44IT_s
#define GAN_MAT_RMULTLIT_S   gan_mat34_rmultl44IT_s
#define GAN_MAT_SLMULTT_Q   gan_mat34_slmultT_q
#define GAN_MAT_TPOSE_I   gan_mat34_tpose_i
#define GAN_MAT_NORMALISE   gan_mat44_normalize
#define GAN_MAT_NORM_FNAME   "gan_mat44_normalize"
#define GAN_MATT_NORMALISE   gan_mat44T_normalize
#define GAN_MATT_NORM_FNAME   "gan_mat44T_normalize"
#define GAN_MATTYPE   Gan_Matrix44
#define GAN_SQUMATTYPE   Gan_SquMatrix44
#define GAN_SQUMATTYPEP   Gan_SquMatrix44
#define GAN_MAT_SCALE_S   gan_mat44_scale_s
#define GAN_MAT_DIVIDE_S   gan_mat44_divide_s
#define GAN_MAT_FNORM_S   gan_mat44_Fnorm_s
#define GAN_SYMMAT_IDENT_S   gan_symmat44_ident_s
#define GAN_SYMMAT_INVERT_Q   gan_symmat44_invert_q
#define GAN_SYMMAT_ZERO_Q   gan_symmat44_zero_q
#define GAN_SYMMAT_MULTV_Q   gan_symmat44_multv4_q
#define GAN_SYMMAT_DIVIDE_S   gan_symmat44_divide_s
#define GAN_SYMMAT_DIVIDE_I   gan_symmat44_divide_i
#define GAN_SYMMAT_INCREMENT   gan_symmat44_increment
#define GAN_SYMMAT_TRACE_S   gan_symmat44_trace_s
#define GAN_SYMMAT_SUB_Q   gan_symmat44_sub_q
#define GAN_SYMMAT_SUMSQR_Q   gan_symmat44_sumsqr_q
#define GAN_SYMMAT_CHOLESKY_Q   gan_symmat44_cholesky_q
#define GAN_SYMMATP_TRACE_S   gan_symmat44_trace_s
#define GAN_SYMMAT_LRMULTM_Q   gan_symmat44_lrmultm44_q
#define GAN_LTMATI_MULTV_S   gan_ltmat44I_multv4_s
#define GAN_MAT_RMULTLIT_S   gan_mat44_rmultl44IT_s
#define GAN_MAT_RMULTLIT_S   gan_mat44_rmultl44IT_s
#define GAN_MAT_SLMULTT_Q   gan_mat44_slmultT_q
#define GAN_MAT_TPOSE_I   gan_mat44_tpose_i

Functions

Gan_Bool gan_mat22_normalize (Gan_Matrix22 *B, int n, double term_threshold, int max_iterations, Gan_SquMatrix22 *Lp)
 Normalize array of 2x2 matrices to identity inertia moment.
Gan_Bool gan_mat22T_normalize (Gan_Matrix22 *B, int n, double term_threshold, int max_iterations, Gan_SquMatrix22 *Lp)
 Normalize array of 2x2 matrices to identity inertia moment.
Gan_Bool gan_mat23_normalize (Gan_Matrix23 *B, int n, double term_threshold, int max_iterations, Gan_SquMatrix33 *Lp)
 Normalize array of 2x3 matrices to identity inertia moment.
Gan_Bool gan_mat24_normalize (Gan_Matrix24 *B, int n, double term_threshold, int max_iterations, Gan_SquMatrix44 *Lp)
 Normalize array of 2x4 matrices to identity inertia moment.
Gan_Bool gan_mat33_normalize (Gan_Matrix33 *B, int n, double term_threshold, int max_iterations, Gan_SquMatrix33 *Lp)
 Normalize array of 3x3 matrices to identity inertia moment.
Gan_Bool gan_mat33T_normalize (Gan_Matrix33 *B, int n, double term_threshold, int max_iterations, Gan_SquMatrix33 *Lp)
 Normalize array of 3x3 matrices to identity inertia moment.
Gan_Bool gan_mat34_normalize (Gan_Matrix34 *B, int n, double term_threshold, int max_iterations, Gan_SquMatrix44 *Lp)
 Normalize array of 3x4 matrices to identity inertia moment.
Gan_Bool gan_mat44_normalize (Gan_Matrix44 *B, int n, double term_threshold, int max_iterations, Gan_SquMatrix44 *Lp)
 Normalize array of 4x4 matrices to identity inertia moment.
Gan_Bool gan_mat44T_normalize (Gan_Matrix44 *B, int n, double term_threshold, int max_iterations, Gan_SquMatrix44 *Lp)
 Normalize array of 4x4 matrices to identity inertia moment.

Function Documentation

Gan_Bool gan_mat22_normalize (  Gan_Matrix22 *  B,
int  n,
double  term_threshold,
int  max_iterations,
Gan_SquMatrix22 *  Lp
) 
 

Normalize array of 2x2 matrices to identity inertia moment.

Parameters:
B array of matrices to normalise
n number of vectors in array
term_threshold termination threshold
max_iterations maximum number of iterations
Lp pointer to solution for triangular normalising matrix
Returns:
GAN_TRUE on success, or GAN_FALSE if the algorithm failed.
This function applies projective normalization to the array of n 2x2 matrices B. After the normalization, the matrices B are transformed by a lower triangular matrix $ L $, and scaled to unit length, so that the transformed vectors

\[ B'_i = \frac{1}{||B_i L^{-{\top}}||_F}(B_i L^{-{\top}}) \]

satisfy the equation

\[ \sum_{i=1\ldots n} ({B'_i}^{\top} B'_i) = \frac{n}{2} I_{2\times 2} \]

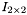where $ I_{2\times 2} $ is the 2x2 identity matrix.

term_threshold specifies a threshold on the smallness of an adjustment to $ L $, below which the algorithm terminates successfully.

max_iterations specifies the maximum number of iterations to perform. If this is reached without the above threshold being reached, the algorithm terminates with failure, returning GAN_FALSE.

Lp is a pointer set to the final solution for the triangular matrix $ L $. If it is passed as NULL then Lp is ignored.

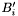Upon successful termination, the matrices B are transformed to $ B'_i $ as shown above, and GAN_TRUE is returned.

See also:
gan_mat22T_normalize, gan_vec2_normalize(), gan_mat22_normalize().

Gan_Bool gan_mat22T_normalize (  Gan_Matrix22 *  B,
int  n,
double  term_threshold,
int  max_iterations,
Gan_SquMatrix22 *  Lp
) 
 

Normalize array of 2x2 matrices to identity inertia moment.

Parameters:
B array of matrices to normalise
n number of vectors in array
term_threshold termination threshold
max_iterations maximum number of iterations
Lp pointer to solution for triangular normalising matrix
Returns:
GAN_TRUE on success, or GAN_FALSE on failure.
This function applies projective normalization to the array of n 2x2 matrices B. After the normalization, the matrices B are transformed by a lower triangular matrix $ L $, and scaled to unit length, so that the transformed vectors

\[ B'_i = \frac{1}{||L^{-1} B_i||_F}(L^{-1} B_i) \]

satisfy the equation

\[ \sum_{i=1\ldots n} (B'_i {B'_i}^{\top}) = \frac{n}{2} I_{2\times 2} \]

where $ I_{2\times 2} $ is the 2x2 identity matrix.

term_threshold specifies a threshold on the smallness of an adjustment to $ L $, below which the algorithm terminates successfully.

max_iterations specifies the maximum number of iterations to perform. If this is reached without the above threshold being reached, the algorithm terminates with failure, returning GAN_FALSE.

Lp is a pointer set to the final solution for the triangular matrix $ L $. If it is passed as NULL then Lp is ignored.

Upon successful termination, the matrices B are transformed to $ B'_i $ as shown above, and GAN_TRUE is returned.

See also:
gan_mat22_normalize(), gan_vec2_normalize(), gan_mat22_normalize().

Gan_Bool gan_mat23_normalize (  Gan_Matrix23 *  B,
int  n,
double  term_threshold,
int  max_iterations,
Gan_SquMatrix33 *  Lp
) 
 

Normalize array of 2x3 matrices to identity inertia moment.

Parameters:
B array of matrices to normalise
n number of vectors in array
term_threshold termination threshold
max_iterations maximum number of iterations
Lp pointer to solution for triangular normalising matrix
Returns:
GAN_TRUE on success, or GAN_FALSE if the algorithm failed.
This function applies projective normalization to the array of n 2x3 matrices B. After the normalization, the matrices B are transformed by a lower triangular matrix $ L $, and scaled to unit length, so that the transformed vectors

\[ B'_i = \frac{1}{||B_i L^{-{\top}}||_F}(B_i L^{-{\top}}) \]

satisfy the equation

\[ \sum_{i=1\ldots n} ({B'_i}^{\top} B'_i) = \frac{n}{3} I_{3\times 3} \]

where $ I_{3\times 3} $ is the 3x3 identity matrix.

term_threshold specifies a threshold on the smallness of an adjustment to $ L $, below which the algorithm terminates successfully.

max_iterations specifies the maximum number of iterations to perform. If this is reached without the above threshold being reached, the algorithm terminates with failure, returning GAN_FALSE.

Lp is a pointer set to the final solution for the triangular matrix $ L $. If it is passed as NULL then Lp is ignored.

Upon successful termination, the matrices B are transformed to $ B'_i $ as shown above, and GAN_TRUE is returned.

See also:
gan_vec3_normalize(), gan_mat33_normalize().

Gan_Bool gan_mat24_normalize (  Gan_Matrix24 *  B,
int  n,
double  term_threshold,
int  max_iterations,
Gan_SquMatrix44 *  Lp
) 
 

Normalize array of 2x4 matrices to identity inertia moment.

Parameters:
B array of matrices to normalise
n number of vectors in array
term_threshold termination threshold
max_iterations maximum number of iterations
Lp pointer to solution for triangular normalising matrix
Returns:
GAN_TRUE on success, or GAN_FALSE if the algorithm failed.
This function applies projective normalization to the array of n 2x4 matrices B. After the normalization, the matrices B are transformed by a lower triangular matrix $ L $, and scaled to unit length, so that the transformed vectors

\[ B'_i = \frac{1}{||B_i L^{-{\top}}||_F}(B_i L^{-{\top}}) \]

satisfy the equation

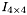\[ \sum_{i=1\ldots n} ({B'_i}^{\top} B'_i) = \frac{n}{4} I_{4\times 4} \]

where $ I_{4\times 4} $ is the 4x4 identity matrix.

term_threshold specifies a threshold on the smallness of an adjustment to $ L $, below which the algorithm terminates successfully.

max_iterations specifies the maximum number of iterations to perform. If this is reached without the above threshold being reached, the algorithm terminates with failure, returning GAN_FALSE.

Lp is a pointer set to the final solution for the triangular matrix $ L $. If it is passed as NULL then Lp is ignored.

Upon successful termination, the matrices B are transformed to $ B'_i $ as shown above, and GAN_TRUE is returned.

See also:
gan_vec4_normalize(), gan_mat44_normalize().

Gan_Bool gan_mat33_normalize (  Gan_Matrix33 *  B,
int  n,
double  term_threshold,
int  max_iterations,
Gan_SquMatrix33 *  Lp
) 
 

Normalize array of 3x3 matrices to identity inertia moment.

Parameters:
B array of matrices to normalise
n number of vectors in array
term_threshold termination threshold
max_iterations maximum number of iterations
Lp pointer to solution for triangular normalising matrix
Returns:
GAN_TRUE on success, or GAN_FALSE if the algorithm failed.
This function applies projective normalization to the array of n 3x3 matrices B. After the normalization, the matrices B are transformed by a lower triangular matrix $ L $, and scaled to unit length, so that the transformed vectors

\[ B'_i = \frac{1}{||B_i L^{-{\top}}||_F}(B_i L^{-{\top}}) \]

satisfy the equation

\[ \sum_{i=1\ldots n} ({B'_i}^{\top} B'_i) = \frac{n}{3} I_{3\times 3} \]

where $ I_{3\times 3} $ is the 3x3 identity matrix.

term_threshold specifies a threshold on the smallness of an adjustment to $ L $, below which the algorithm terminates successfully.

max_iterations specifies the maximum number of iterations to perform. If this is reached without the above threshold being reached, the algorithm terminates with failure, returning GAN_FALSE.

Lp is a pointer set to the final solution for the triangular matrix $ L $. If it is passed as NULL then Lp is ignored.

Upon successful termination, the matrices B are transformed to $ B'_i $ as shown above, and GAN_TRUE is returned.

See also:
gan_mat33T_normalize, gan_vec3_normalize(), gan_mat33_normalize().

Gan_Bool gan_mat33T_normalize (  Gan_Matrix33 *  B,
int  n,
double  term_threshold,
int  max_iterations,
Gan_SquMatrix33 *  Lp
) 
 

Normalize array of 3x3 matrices to identity inertia moment.

Parameters:
B array of matrices to normalise
n number of vectors in array
term_threshold termination threshold
max_iterations maximum number of iterations
Lp pointer to solution for triangular normalising matrix
Returns:
GAN_TRUE on success, or GAN_FALSE on failure.
This function applies projective normalization to the array of n 3x3 matrices B. After the normalization, the matrices B are transformed by a lower triangular matrix $ L $, and scaled to unit length, so that the transformed vectors

\[ B'_i = \frac{1}{||L^{-1} B_i||_F}(L^{-1} B_i) \]

satisfy the equation

\[ \sum_{i=1\ldots n} (B'_i {B'_i}^{\top}) = \frac{n}{3} I_{3\times 3} \]

where $ I_{3\times 3} $ is the 3x3 identity matrix.

term_threshold specifies a threshold on the smallness of an adjustment to $ L $, below which the algorithm terminates successfully.

max_iterations specifies the maximum number of iterations to perform. If this is reached without the above threshold being reached, the algorithm terminates with failure, returning GAN_FALSE.

Lp is a pointer set to the final solution for the triangular matrix $ L $. If it is passed as NULL then Lp is ignored.

Upon successful termination, the matrices B are transformed to $ B'_i $ as shown above, and GAN_TRUE is returned.

See also:
gan_mat33_normalize(), gan_vec3_normalize(), gan_mat33_normalize().

Gan_Bool gan_mat34_normalize (  Gan_Matrix34 *  B,
int  n,
double  term_threshold,
int  max_iterations,
Gan_SquMatrix44 *  Lp
) 
 

Normalize array of 3x4 matrices to identity inertia moment.

Parameters:
B array of matrices to normalise
n number of vectors in array
term_threshold termination threshold
max_iterations maximum number of iterations
Lp pointer to solution for triangular normalising matrix
Returns:
GAN_TRUE on success, or GAN_FALSE if the algorithm failed.
This function applies projective normalization to the array of n 3x4 matrices B. After the normalization, the matrices B are transformed by a lower triangular matrix $ L $, and scaled to unit length, so that the transformed vectors

\[ B'_i = \frac{1}{||B_i L^{-{\top}}||_F}(B_i L^{-{\top}}) \]

satisfy the equation

\[ \sum_{i=1\ldots n} ({B'_i}^{\top} B'_i) = \frac{n}{4} I_{4\times 4} \]

where $ I_{4\times 4} $ is the 4x4 identity matrix.

term_threshold specifies a threshold on the smallness of an adjustment to $ L $, below which the algorithm terminates successfully.

max_iterations specifies the maximum number of iterations to perform. If this is reached without the above threshold being reached, the algorithm terminates with failure, returning GAN_FALSE.

Lp is a pointer set to the final solution for the triangular matrix $ L $. If it is passed as NULL then Lp is ignored.

Upon successful termination, the matrices B are transformed to $ B'_i $ as shown above, and GAN_TRUE is returned.

See also:
gan_vec4_normalize(), gan_mat44_normalize().

Gan_Bool gan_mat44_normalize (  Gan_Matrix44 *  B,
int  n,
double  term_threshold,
int  max_iterations,
Gan_SquMatrix44 *  Lp
) 
 

Normalize array of 4x4 matrices to identity inertia moment.

Parameters:
B array of matrices to normalise
n number of vectors in array
term_threshold termination threshold
max_iterations maximum number of iterations
Lp pointer to solution for triangular normalising matrix
Returns:
GAN_TRUE on success, or GAN_FALSE if the algorithm failed.
This function applies projective normalization to the array of n 4x4 matrices B. After the normalization, the matrices B are transformed by a lower triangular matrix $ L $, and scaled to unit length, so that the transformed vectors

\[ B'_i = \frac{1}{||B_i L^{-{\top}}||_F}(B_i L^{-{\top}}) \]

satisfy the equation

\[ \sum_{i=1\ldots n} ({B'_i}^{\top} B'_i) = \frac{n}{4} I_{4\times 4} \]

where $ I_{4\times 4} $ is the 4x4 identity matrix.

term_threshold specifies a threshold on the smallness of an adjustment to $ L $, below which the algorithm terminates successfully.

max_iterations specifies the maximum number of iterations to perform. If this is reached without the above threshold being reached, the algorithm terminates with failure, returning GAN_FALSE.

Lp is a pointer set to the final solution for the triangular matrix $ L $. If it is passed as NULL then Lp is ignored.

Upon successful termination, the matrices B are transformed to $ B'_i $ as shown above, and GAN_TRUE is returned.

See also:
gan_mat44T_normalize, gan_vec4_normalize(), gan_mat44_normalize().

Gan_Bool gan_mat44T_normalize (  Gan_Matrix44 *  B,
int  n,
double  term_threshold,
int  max_iterations,
Gan_SquMatrix44 *  Lp
) 
 

Normalize array of 4x4 matrices to identity inertia moment.

Parameters:
B array of matrices to normalise
n number of vectors in array
term_threshold termination threshold
max_iterations maximum number of iterations
Lp pointer to solution for triangular normalising matrix
Returns:
GAN_TRUE on success, or GAN_FALSE on failure.
This function applies projective normalization to the array of n 4x4 matrices B. After the normalization, the matrices B are transformed by a lower triangular matrix $ L $, and scaled to unit length, so that the transformed vectors

\[ B'_i = \frac{1}{||L^{-1} B_i||_F}(L^{-1} B_i) \]

satisfy the equation

\[ \sum_{i=1\ldots n} (B'_i {B'_i}^{\top}) = \frac{n}{4} I_{4\times 4} \]

where $ I_{4\times 4} $ is the 4x4 identity matrix.

term_threshold specifies a threshold on the smallness of an adjustment to $ L $, below which the algorithm terminates successfully.

max_iterations specifies the maximum number of iterations to perform. If this is reached without the above threshold being reached, the algorithm terminates with failure, returning GAN_FALSE.

Lp is a pointer set to the final solution for the triangular matrix $ L $. If it is passed as NULL then Lp is ignored.

Upon successful termination, the matrices B are transformed to $ B'_i $ as shown above, and GAN_TRUE is returned.

See also:
gan_mat44_normalize(), gan_vec4_normalize(), gan_mat44_normalize().

Generated on Fri Mar 17 12:44:58 2006 by  doxygen 1.3.9.1