Hough Transform
[Vision Package]

Classes
struct	FHT_Path
struct	FHT_Path
Defines
#define	DEBUG   1
#define	gel(M, i, j)   gan_mat_get_el(M,i,j)
Typedefs
typedef FHT_Path	FHT_Path
typedef FHT_Path	FHT_Path
Functions
Gan_Bool	gan_fast_hough_transform (int k, Gan_Matrix *a, int *weight, int no_points, double *S0, double *X0, int max_level, int T_thres, Gan_MemoryStack *memory_stack, double *X_best, int *level_best, int *accum_best, Gan_BitArray *list_best, int *subdivs)
	General purpose Fast Hough Transform (FHT) function.
Gan_Bool	gan_modified_fht2D (double *x, double *y, int *weight, int no_points, double m_range, double c_range, double c_root, int max_level, int T_thres, Gan_MemoryStack *memory_stack, double *m_best, double *c_best, int *level_best, int *accum_best, Gan_BitArray *list_best)
	General purpose FHT line finder function.

---

Function Documentation

Gan_Bool gan_fast_hough_transform (  int  k, Gan_Matrix *  a, int *  weight, int  no_points, double *  S0, double *  X0, int  max_level, int  T_thres, Gan_MemoryStack *  memory_stack, double *  X_best, int *  level_best, int *  accum_best, Gan_BitArray *  list_best, int *  subdivs )

General purpose Fast Hough Transform (FHT) function. Parameters: k  Dimensionality of parameter space a  Feature space (k+1)-vectors arranged as a matrix weight  Weights assigned to each feature vector no_points  Number of data points S0  Half-range of parameters X0  Centre of parameter ranges max_level  Maximum subdivision level T_thres  Threshold T in FHT for deciding whether subdivide or not memory_stack  Pointer to memory stack structure X_best  Output best-fit parameters level_best  Output subdivision level reached by FHT accum_best  Output sum of weights of points with lines intersecting final hypersphere list_best  Output bit array bit-list, with 1's for points involved in best-fit result subdivs  Output total number of subdivisions Returns: GAN_TRUE on success, GAN_FALSE on failure. For each feature point j the relationship between feature space uses parametrisation (not normalised) where X[i] are the parameters and k is the dimensionality of parameter space. The starting parameter half-ranges are given by the S0 vector, and the parameter origin by the X0 vector. S0 and X0 thus define the root hypercube: This is a depth-first version of the FHT, i.e. the child hypercubes are subdivided exhaustively before trying another child. This minimises memory requirement by limiting it to a contains feature space (k+1)-vectors arranged as a no_points by k+1 matrix.

Gan_Bool gan_modified_fht2D (  double *  x, double *  y, int *  weight, int  no_points, double  m_range, double  c_range, double  c_root, int  max_level, int  T_thres, Gan_MemoryStack *  memory_stack, double *  m_best, double *  c_best, int *  level_best, int *  accum_best, Gan_BitArray *  list_best )

General purpose FHT line finder function. Parameters: x  Array of x-coordinates of data points y  Array of y-coordinates of data points weight  Array of weights assigned to each point no_points  Number of data points m_range  Range of line gradient c_range  Range of line intercept c_root  Centre point of intercept for root hypercube max_level  Maximum subdivision level T_thres  Threshold T in FHT for deciding whether to subdivide memory_stack  Pointer to memory stack structure m_best  Output gradient of best-fit line c_best  Output intercept of best-fit line level_best  Output subdivision level reached by FHT accum_best  Output sum of weights of points with lines intersecting final hypersphere list_best  Output bit-list, with 1's for points involved in best-fit result Uses parametrisation where 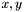are the coordinates of a point on a plane and 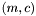are gradient/intercept line parameters. 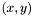Each point can be thought of as defining a line in space, each point on the line in space representing a line in space passing through the point . 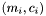The FHT starts with a root "hypercube" (in this case a rectangle) in space defined by and subdivides into 2x2 "child" hypercubes, checking each child to see whether enough lines (greater than a threshold) intersect a hypersphere circumscribed around the hypercube. In fact the slightly more general approach here allows a weight to be assigned to each point, and the threshold is applied to the sum of weights of intersecting lines. This is a depth-first version of the FHT, i.e. the child hypercubes are subdivided exhaustively before trying another child. This minimises memory requirement by limiting it to

---